Baseline model using logistic regression
The notebook used to develop this baseline model can be found here.
Summary
As an initial baseline model, against which we could compare the results of our subsequent models, we attempted to predict crime types using only latitude and longitude (lat and lon) as our predictors. To accomplish this, we ran a multinomial logistic model with no regularization. And we ran it both with and then without “balanced” class weightings for comparison. Given the heavy spatial mixing of crime-type classes as shown in our initial training data EDA we had very low expectations for the quality of predictions that might be generated using only geo-spatial coordinates as our predictors.
Model parameters
For comparison the parameters of the two scikit-learn LogisticRegression model objects fitted for our baseline model are:
MODEL 1: Without balanced class weights
LogisticRegression(C=100000, class_weight=None, dual=False,
fit_intercept=True, intercept_scaling=1,
l1_ratio=None, max_iter=1000,
multi_class='multinomial', n_jobs=None,
penalty='l2', random_state=20, solver='lbfgs',
tol=0.0001, verbose=0, warm_start=False)
MODEL 2: With balanced class weights
LogisticRegression(C=100000, class_weight=None, dual=False,
fit_intercept=True, intercept_scaling=1,
l1_ratio=None, max_iter=1000,
multi_class='multinomial', n_jobs=None,
penalty='l2', random_state=20, solver='lbfgs',
tol=0.0001, verbose=0, warm_start=False)
Model accuracy and AUC
Ultimately, these models resulted in the following training accuracies and average AUCs. As we can see the model generated without using balanced class weights acheived only a TEST accuracy of just 0.2733, which is not surprising given the expected difficulty of predicting crime types given our previous exploration of this data. However, what is interesting is the far lower TEST accuracy for the Model 2, generated using balanced class weights. Surprisingly, the AUC of Model 2 suffers very little as a result of balancing class weights, which leads us to further inspect the prediction results generated by each model in the next section below.
MODEL 1: Without balanced class weights
This model resulted in the following accuracy:
Training 0.2706
Test 0.2733
The model AUC is:
weighted unweighted
Training 0.5519 0.5396
Test 0.5558 0.5370
MODEL 2: With balanced class weights
This model resulted in the following accuracy:
Training 0.1295
Test 0.1332
The model AUC is:
weighted unweighted
Training 0.5487 0.5382
Test 0.5529 0.5395
Model predictions
By viewing the number of predictions generated by each version of the model, we can see that Model 2 generated a more balanced set of predictions, whereas Model 1 only predicted occurances of crime-type classes 4 (harassment-disturbance) and 6 (theft), two of the most heavily over-represented classes in our training set. Even with some many false negative predicted for all other classes in Model 1, because these two classes together represent 43% of our total true TEST observations, this would explain why were able to achieve the TEST accuracy score we did with that model. Likewise, because Model 2 predictions are distributed among all potential response classes, the heavy over-representation of crime-type classes 0 (other) and 4 in our results very negatively impacts overall accuracy on the test set.
MODEL 1: Without balanced class weights
The number of classes predicted by class are:
TRAINING
count proportion
class
4 15446 0.120341
6 112906 0.879659
TEST
count proportion
class
4 3939 0.122756
6 28149 0.877244
MODEL 2: With balanced class weights
The number of classes predicted by class are:
TRAINING
count proportion
class
0 53841 0.419479
1 6662 0.051904
2 1595 0.012427
3 2222 0.017312
4 52740 0.410901
5 3164 0.024651
6 3877 0.030206
7 1837 0.014312
8 2414 0.018808
TEST
count proportion
class
0 13476 0.419970
1 1624 0.050611
2 423 0.013182
3 527 0.016424
4 13313 0.414890
5 763 0.023778
6 964 0.030042
7 409 0.012746
8 589 0.018356
To further understand this effect, we can look at the confusion matrices and resulting classification metrics generated by the TEST results of each model as are shown below. Here again we can see the result of Model 2 predicting a larger number of response classes for the TEST set. For example, the true positive rate (TPR) shown for crime-type 6 in Model 1 is 0.905, but in Model 2 TPR for this same class drops to just 0.026. Because crime-type 6 is our most heavily represented class in our actual TEST data, this metric too supports the discrepancy in Model 1 versus Model 2 accuracy results that we have seen.
MODEL 1: Without balanced class weights
The resulting confusion matrix:
TEST
Actual 0 1 2 3 4 5 6 7 8 Total
Predicted
0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0 0
2 0 0 0 0 0 0 0 0 0 0
3 0 0 0 0 0 0 0 0 0 0
4 127 154 329 357 954 105 824 458 631 3939
5 0 0 0 0 0 0 0 0 0 0
6 1453 1262 2942 2040 4238 751 7815 2969 4679 28149
7 0 0 0 0 0 0 0 0 0 0
8 0 0 0 0 0 0 0 0 0 0
Total 1580 1416 3271 2397 5192 856 8639 3427 5310 32088
The classification metrics derived from the confusion matrix are:
TEST
TP FP FN TN TPR FNR FPR TNR
class
0 0 0 1580 30508 0.000 1.000 0.000 1.000
1 0 0 1416 30672 0.000 1.000 0.000 1.000
2 0 0 3271 28817 0.000 1.000 0.000 1.000
3 0 0 2397 29691 0.000 1.000 0.000 1.000
4 954 2985 4238 23911 0.184 0.816 0.111 0.889
5 0 0 856 31232 0.000 1.000 0.000 1.000
6 7815 20334 824 3115 0.905 0.095 0.867 0.133
7 0 0 3427 28661 0.000 1.000 0.000 1.000
8 0 0 5310 26778 0.000 1.000 0.000 1.000
MODEL 2: With balanced class weights
The resulting confusion matrix:
TEST
Actual 0 1 2 3 4 5 6 7 8 Total
Predicted
0 697 479 1532 1088 1207 394 4715 1245 2119 13476
1 102 85 97 98 353 50 383 173 283 1624
2 21 21 27 30 85 6 120 46 67 423
3 29 24 24 28 99 16 125 73 109 527
4 525 675 1246 974 3041 320 2690 1572 2270 13313
5 41 46 122 51 101 25 155 79 143 763
6 114 32 112 62 133 25 222 100 164 964
7 16 30 30 25 79 8 88 64 69 409
8 35 24 81 41 94 12 141 75 86 589
Total 1580 1416 3271 2397 5192 856 8639 3427 5310 32088
The classification metrics derived from the confusion matrix are:
TEST
TP FP FN TN TPR FNR FPR TNR
class
0 697 12779 883 17729 0.441 0.559 0.419 0.581
1 85 1539 1331 29133 0.060 0.940 0.050 0.950
2 27 396 3244 28421 0.008 0.992 0.014 0.986
3 28 499 2369 29192 0.012 0.988 0.017 0.983
4 3041 10272 2151 16624 0.586 0.414 0.382 0.618
5 25 738 831 30494 0.029 0.971 0.024 0.976
6 222 742 8417 22707 0.026 0.974 0.032 0.968
7 64 345 3363 28316 0.019 0.981 0.012 0.988
8 86 503 5224 26275 0.016 0.984 0.019 0.981
Receiver operator characteristic (ROC) curves by model and class
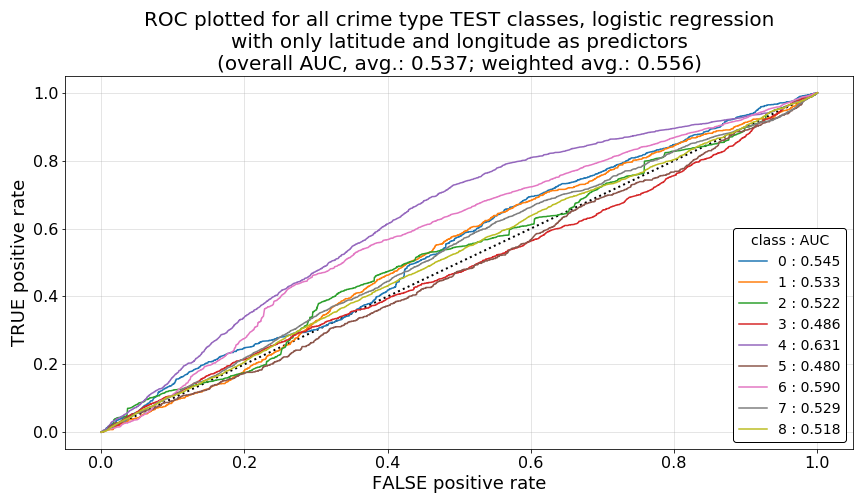
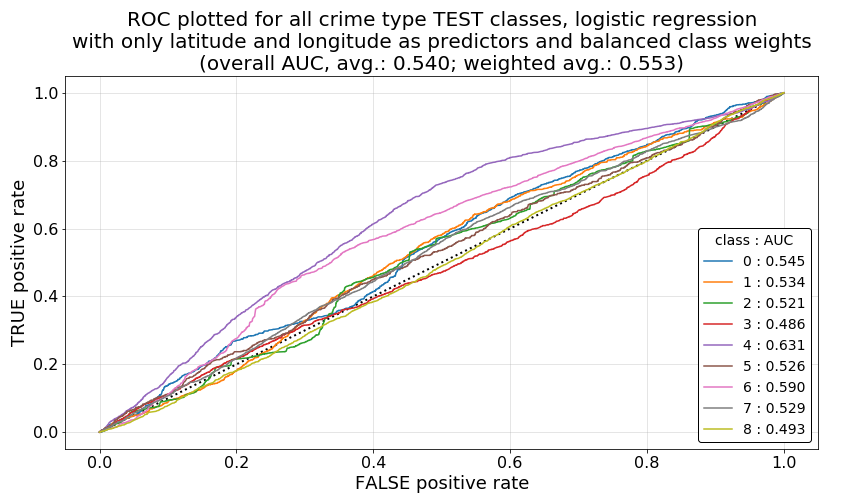
As a final set of items we will investigate to better understand these quality of our results and the differences that we are seeing between Model 1 and Model 2, we will now plot the ROC for each model and class, and report on the individual AUC values by class and model.
As we can see in the first two plots below, ROC curve plotted by class for each model shows very similar results among Model 1 and Model 2 (plotted in that order below), explaining the very similar average overall AUC for both models (note that this metric is also reported on the plots). However, what is evident in both of these models are the unfavorable overall ROC curve shapes for all classes, even the best performing class, crime-type class 4. What we would hope to see here are ROC curves rising very steeply toward a true positive rate (TPR) of 1.0 at very low values for the corresponding false positive rates (FPR), idealing forming a very high, far left, sharp elbow in each curve. Such a curve would indicate that, by modifying our classification probability thresholds for each class (or a particular class of interest, such as violence-aggression) there would be a very low trade-off in FPR to achieve higher TPRs for individual class predictions. A good illustrative example of this this relationship can be seen on the related Wikipedia article, most notably in the illustrative image located here.
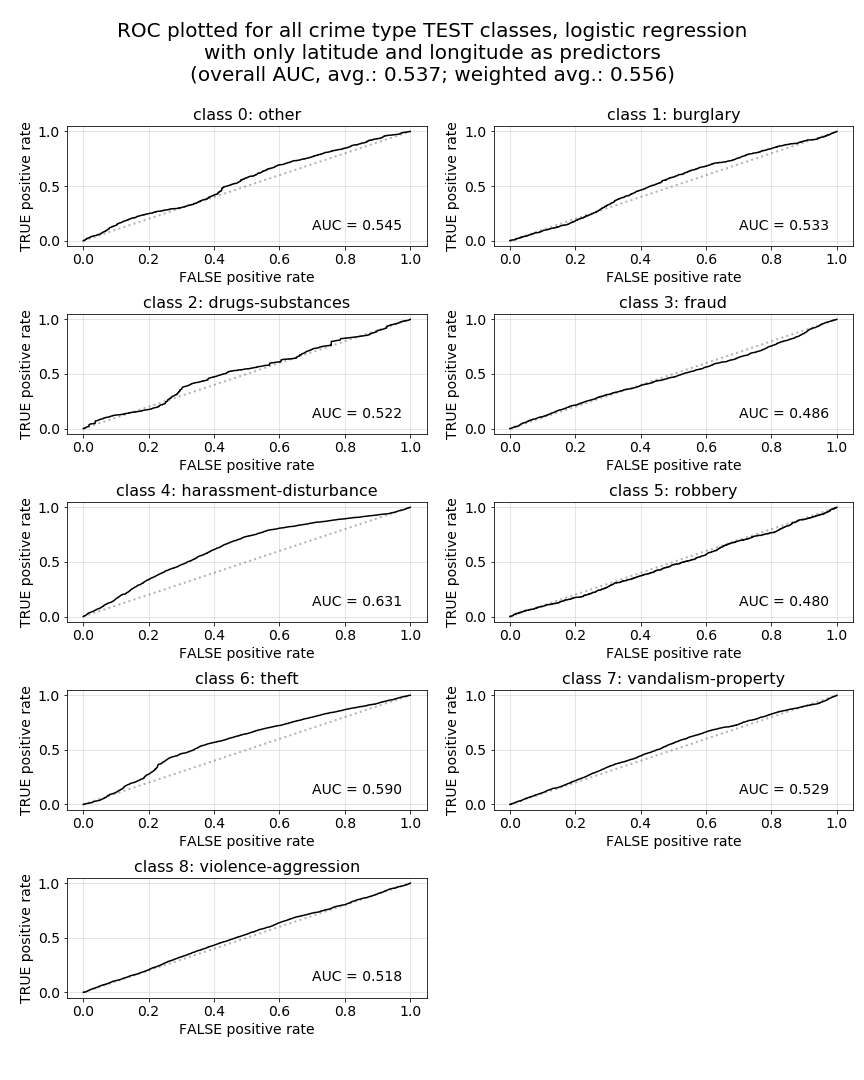
However, what we see in our plots below are wavering ROC curves with very low rates of increase across each plot. Notably, some class ROC curves are even at or below the 0.5 AUC threshold, as is indicated by curved below the diagonal dashed black line plotted as a point of interest in each figure. This particular relationship to the AUC=0.5 reference line can be more easily seen in the third plot below, which breaks out ROC curves for each individual crime-type class for Model 1 as a visual example. Ideally, in future models, would like to see each of these curves pulled upward, toward the left, and away from that 0.5 AUC dashed line as far as possible, which would indicate more favorable opportunities for increasing TPR for particular crime-type classes of interest.
Conclusion and next steps
As expected from our initial EDA and data visualization efforts, due to the heavy spatial mixing of crime-type classes, we have achieved very low accuracy scores and far less than favorable AUC values and ROC curves with the two versions of our baseline model above. What’s also interesting is the sharp decrease in accuracy we achieve when balancing the class weights of our fitted model as discussed above. These are both challenges we will seek to address in our subsequent models.
To some degree, we expect that logistic regression will fail to adequately separate prediction classes due to the linear nature of the model, and that we will eventually find better results by using non-parametric methods such as k-Nearest Neighbors classifiers or Decision Tree-based classifiers, which can provide more flexible decision boundaries. However, after viewing these results, we were still very interested to see what additional predictive accuracy we could achieve and how different our AUC and ROC results might be once we add in a more complete predictor set. To view the results of our subsequent Logistic Regression classifier models in which we generated predictions using the entire set of predictors, please see the Logistic Regression Classifiers summary page. As you can see on that page, we were able to achieve some very interesting results, even with just logistic regression as our classifier.